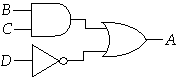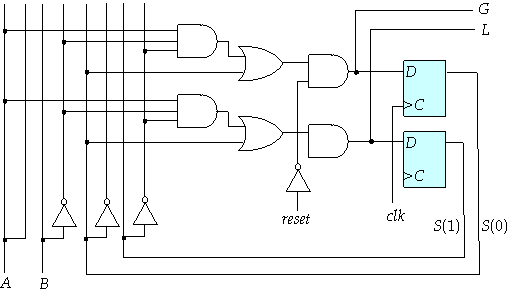Designing Circuits with VHDL
1. Introduction
VHDL is a hardware description language that can be used to
design digital logic circuits. VHDL specifications can be automatically
translated by circuit synthesizers into digital circuits, in
much the same way that Java or C++ programs are translated by compilers
into machine language. While VHDL code bears a superficial resemblance
to programs in conventional sequential programming languages, the
meaning of VHDL code differs in important ways from sequential
programs. Ultimately, the meaning of a VHDL specification is a
circuit, while the meaning of an ordinary
program is the sequential execution of the program statements. The
underlying notion of sequential execution is so pervasive in ordinary
programming that it is easy to take it for granted. In VHDL, on the
other hand, there is no built-in concept of sequential execution and
this can be the source of much misunderstanding when first learning the
language. Understanding the differences between circuit design in VHDL
and conventional programming is one of the key steps in learning to
use the language. Don't worry. You're not expected to understand these
differences yet, but you should be aware of them. As we go along,
you'll
recognize and start to appreciate the differences and their
implications.
2. Combinational Circuits
Signal Assignments in VHDL
Combinational circuits can be represented by
circuit schematics using logic gates. For example,
Equivalently, we can represent this circuit by the Boolean equation A
= BC + D´. VHDL
allows us to specify circuits with equations in much the same way.
A
<= (B and C) or (not D);
Here, A, B, C and D are names of VHDL signals; <= is the concurrent
signal assignment operator and the keywords and, or and not are the familiar
logical operators. The parentheses are used to determine the order of
operations (in this case, they are are not strictly necessary,
but do help make the meaning more clear) and the semicolon terminates
the assignment. A combinational circuit can have multiple outputs,
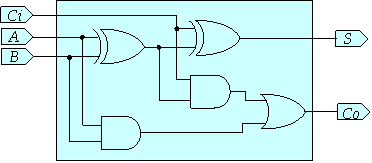
as in the full adder shown below.
We can represent this with a pair of Boolean equations or the
equivalent VHDL signal assignments.
S <=
A xor B xor Ci;
Co <= (A and B) or ((A xor B) and Ci);
In general, a logic circuit with n outputs can be represented
by n signal assignments. The signal
assignments are only part of a VHDL specification. Here is the complete
specification of the full adder.
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
entity fullAdder is
port( A,B: in std_logic; -- input
bits for this stage
Ci: in std_logic; -- carry into this stage
S: out std_logic; -- sum bit
Co: out std_logic -- carry out of this stage
);
end
fullAdder;
architecture a1 of
fullAdder is
begin
S <= A xor B xor Ci;
Co <= (A and B) or ((A
xor B) and Ci);
end a1;
The first four lines specify a library of standard definitions. We'll
just treat this as a required part of the specification, without going
into details. The next group of seven lines is the entity
declaration for our full adder circuit. The entity declaration
defines the name of the circuit (fullAdder), its inputs
and outputs and their types (std_logic). The inputs
and outputs are specified in a port list. Successive elements
of the port list are separated by semicolons (note that there is
no semicolon following the last element). A pair of dashes introduces a
comment, which continues to the end of the line. Comments don't
affect the meaning of the specification, but are essential for making
it readable by other people. It's a good idea to use comments to
identify the inputs and outputs of your circuits, document what
your circuits do and how they work. Get in the habit of documenting all
your code. The last five lines above, constitute the architecture
specification, which includes our two signal assignments. VHDL
permits you to have multiple architectures for the same entity, hence
the architecture has its own label, separate from the entity name.
It's important to understand the distinction between the entity
declaration and the architecture. The entity declaration defines the
name of the circuit and the architecture defines its implementation. In
a block diagram or
"abridged" schematic, we often show a portion of a larger circuit as a
block with labeled inputs and outputs, as illustrated below for the fullAdder.
This corresponds directly to the entity declaration. When we supplement
such a diagram, by filling in the block with an appropriate schematic,
we are specifying an architecture.
In the fullAdder
specification, all the signals are either inputs or outputs. We can
also have internal signals, much as we have internal variables in
ordinary programming languages. For example, we could write the fullAdder architecture
this way.
architecture a1 of fullAdder is
signal X: std_logic;
begin
X <= A
xor B;
S <=
X xor Ci;
Co <= (A and B) or (X and Ci);
end a1;
The signal declaration is required and specifies the type of X. VHDL is a strongly
typed language and requires that signals have the proper types.
Signal declarations appear before the begin keyword of the
architecture. The diagram for this architecture shown below, also
includes the signal X
explicitly and the use of X in both of the output
signals. Note that the order of the signal assignments, in this case,
has no effect on the meaning of the specification. In particular, if we
put the assignment to X
last, the resulting circuit would be exactly the same. This may seem
strange, but it illustrates how VHDL is different from ordinary
programming. The signal assignments are Boolean equations specifying
logic circuits. The order in which
you write the equations does not affect the meaning of the circuit
any more than the way you draw the corresponding schematic diagram
affects how it works.
VHDL also lets us define and use vectors of signals.
architecture
a1 of vecExample is
signal a, b: std_logic_vector(0 to 7);
signal c: std_logic_vector(7 downto 0);
begin
b <= "10101010"; -- double
quotes used for arrays of bits
a <=
b and "00011111";
c <= a(4 to 7) & b(0 to 3);
end
a1;
The std_logic_vector
type can have indices that either increase or decrease in value as you
go from "left-to-right". The direction of the indices affects how
assignments involving vectors are interpreted, as we will see shortly.
For signals that are used to represent numerical values,
it's usual to have the indices decrease. A signal assignment involving
logic vectors can be thought of as just a short hand for a group of
signal assignments. For example, the first assignment above is
equivalent to
b(0)
<= '1'; b(1)
<= '0'; b(2)
<= '1'; b(3)
<= '0';
b(4)
<= '1'; b(5)
<= '0'; b(6)
<= '1'; b(7)
<= '0';
Here, the notation b(i)
refers to the individual elements of the vector. In the second
assignment, the and operator
is applied bit-wise, so the meaning of the assignment is
a(0) <= b(0) and '0'; a(1) <= b(1) and '0';
a(2) <=
b(2) and '0'; a(3) <= b(3) and '1';
a(4) <=
b(4) and '1'; a(5) <= b(5) and '1';
a(6) <=
b(6) and '1'; a(7) <= b(7) and '1';
The last assignment refers to sub-vectors of a and b and uses the concatenation
operator &.
Also note that the indices for c run in the opposite
order of the indices for a
and b, so the
meaning of this assignment is
c(7) <=
a(4); c(6) <= a(5); c(5) <= a(6); c(4) <= a(7);
c(3) <=
b(0); c(2) <= b(1); c(1) <= b(2); c(0) <= b(3);
In principal, we can define any combinational logic circuit using just
simple signal assignments. In more complex circuits it's convenient to
have higher level constructs. The conditional signal assignment
allows us to make the value assigned to a signal dependent on a series
of conditions.
entity
conditionalExample is
port(a, b, c: in std_logic; d: out std_logic);
end conditionalExample;
architecture a1 of conditionalExample is
begin
d <= '1' when a = b else
b
when b /= c else
a xor c;
end a1;
The comparison operators '='
and '/=' in
the when clauses are true if the two operands are equal or not
equal, respectively. The conditional signal assignment is not strictly
necessary, since the following ordinary assignment is equivalent.
d <= ((a xnor b) and '1')
or
(not (a xnor b) and (b
xor c) and b) or
(not (a xnor b) and
not (b xor c) and (a xor c));
While VHDL allows the comparison operators in the condition part
of the when clauses, they cannot be used
in ordinary assignments, but the xnor and xor operations can
serve the same purpose. Note the pattern of the transformation from the
conditional assignment to the ordinary assignment. Overall, the new
expression is the logical-or of several sub-expressions, one for each
part of
the conditional assignment. Each sub-expression is the logical-and
of the condition in one of the when clauses, the complement of the
conditions in the previous when clauses and the value associated with
the 'current' clause. Of course, we could also simplify this
expression, giving
d <=
not(a and (not b)
and c);
but it's certainly easier to let the synthesizer do the logic
simplification so that we can concentrate on the higher level meaning
of the circuit. The conditional assignment is one
tool for allowing us to express the circuit behavior at a somewhat
higher level. The general form of the conditional assignment is
x<= value1 when condition1 else
value2 when condition2 else
value3 when condition3 else
... else
valuen
Each of the values must have the same type as the signal
on the left side of the assignment. Each of the conditions is a Boolean
function on some set of variables. The equivalent form of ordinary
signal assignment is
x<= (condition1
and value1) or
(not condition1
and condition2
and value2) or
(not condition1
and not condition2
and condition3
and value3) or
...
(not condition1
and ... and not conditionn-1
and valuen)
We can also have conditional signal assignments involving logic
vectors. For example, if x,
a, b and c all have type std_logic_vector(3 down to 0)
and s has type std_logic_vector(1 downto 0),
we can write
x <=
a when s = "00"
else
a and b when s = "01"
else
a xor c when s = "10"
else
b;
As with ordinary signal assignments, we can view this as a short-hand
for four separate signal assignments operating on individual signals.
x(3)
<= a(3) when s(1) = '0'
and s(0) = '0' else
a(3) and b(3) when s(1) = '0'
and s(0) = '1' else
a(3) xor c(3) when s(1) = '1'
and s(0) = '0' else
b(3);
x(2)
<= a(2) when s(1) = '0'
and s(0) = '0' else
a(2) and b(2) when s(1) = '0'
and s(0) = '1' else
a(2) xor c(2) when s(1) = '1'
and s(0) = '0' else
b(2);
and so forth. Note that because the conditions in this case just
enumerate the different values of the signal s, the circuit
specified by the statement can be implemented with a 4:1 multiplexor
with a four bit wide data path.
Processes and Conditional Statements
VHDL provides a variety of higher level constructs that make it easier
to express more complex designs. In particular, it includes an if-then-else construct,
similar to those in ordinary programming languages. For example, we can
write
if a = '0' then
x
<= a; y <= b;
elsif a = b then
x
<= '0'; y <= '1';
else
x
<= not b; y <= not b;
end if;
VHDL requires that higher level constructs like the if-then-else be used
only inside a process block. So the complete architecture for a
module with inputs a, b and outputs x, y that includes the
above
logic would be
architecture a1 of
ifThenExample
is
begin
process(a,b)
begin
if a = '0' then
x
<= a; y <= b;
elsif a = b
then
x <= '0'; y <= '1';
else
x <= not b; y
<= not b;
end if;
end process
end a1;
Following the process
keyword is a
list of signal names, which is called the sensitivity list. The
sensitivity list should include all signals that can trigger changes to
signals that are assigned values within the process. If we're using the
process to define a combinational circuit, this means that the
sensitivity list should include all signals that appear in any
expression within the process. Note that we could have specified a
circuit with
the same behavior using two conditional assignment statements, one
for x and one for y. Or, we could have
written them using two ordinary signal assignments. For this simple
example, those alternatives might be preferable, but for more complex
circuits, the use of the if-then-else
construct can make it easier to express the logic you have in
mind and easier for others to read and understand your VHDL code.
There is an important rule that must be followed
when using a process to define a combinational circuit.
Every signal that is assigned a value inside a process
must be defined for all possible conditions.
The process above satisfies this condition, but the following version
does not.
architecture a1 of
ifThenExample
is
begin
process(a,b)
begin
if a = '0' then
x
<= a ; y <= b;
elsif a = b
then
x <= '0'; y
<= '1';
else
x <= not b;
-- y not defined when a=1, b=0
end if;
end process
end a1;
While this is a legitimate VHDL specification, it does not correspond
to any combinational circuit. The reason for this is that VHDL defines
the value of a signal to be unchanged by a process if its value is not
specified under some condition. So in this case, the value of y would not change when a=1 and b=0. To create
a circuit that has this behavior, the synthesizer must provide a
storage element (typically a latch) to retain the value of y in this case. The
circuit shown below has the specified behavior:
So if you are intending to implement a combinational circuit, it's
important to pay attention to this rule. If you
don't, the circuit synthesized for your specification will contain
storage elements that may cause it to behave differently than you
intended. It's easy to violate this rule and it can be hard to figure
out what's wrong when you do, so be aware of it and try to adopt coding
practices that will keep you from making such mistakes. One simple
way to avoid the problem is to always start your process with
assignments of default values for all signals that are assigned
a value
within the process. For example, we could write
architecture a1 of
ifThenExample
is
begin
process(a,b)
begin
x <= '0'; y
<= '0'; -- default values for x, y
if a = '0' then
x
<= a; y <= b;
elsif a = b
then
x <= '0'; y <= '1';
else
x <= not a; --
y=0 when a=1, b=0
end if;
end process
end a1;
Now, if you intended to write the original
version of this code, the above specification would still
be incorrect, but at least it specifies a combinational circuit and
you'll have an easier time figuring out what you did wrong than you
would if the circuit had a "hidden" storage element.
Note that for the above code to work as intended, the assignments of
the default values must come before the if-then-else. This is a
case where statement order matters. While the effect of statement order
is similar to that in ordinary programming languages, the
underlying reasons are a little different, since in VHDL, there
is no built-in concept of sequential execution. Whenever there
are two assignments to the same variable the later one takes precedence
in all conditions allowed by the context in which it appears. So
for example, in this architecture
architecture a1 of foo is
begin
process(a,b)
begin
c <= '0';
if a = b then
c
<= '1';
end if;
end process
end a1;
the first assignment to c
applies no matter what values a and b have, while the second
applies only when a=b.
Because the second assignment comes after the first one, it overrides
the first, when a=b.
If we wrote
architecture a1 of foo is
begin
process(a,b)
begin
if a = b then
c
<= '1';
end if;
c <= '0';
end process
end a1;
the resulting circuit would make c=0, not matter what
value a and b had. While the first
version is equivalent to
architecture a1 of foo is
begin
c <= a
xnor b;
end a1;
the second is equivalent to
architecture a1 of foo is
begin
c <= '0';
end
a1;
The implications of statement order within a VHDL process are a
little bit tricky. To explore this issue further, suppose we have the
following signal assignments in a VHDL specification within a process.
A <=
'1'; -- '1' denotes the constant logic value 1
B <= A;
A <= '0'; -- '0' denotes the constant
logic value 0
If these were assignments in a sequential language, the value assigned
to B would be 1. However, in
VHDL, B's
value is 0.
Why? The key to this is understanding how VHDL interprets the two
assignments to A.
The first assignment says that the signal A is wired to a constant
value of 1 in
the logic circuit defined by the code. The second says that A is wired a constant
value of 0.
They can't both be true, so how does VHDL interpret these two
contradictory statements? While it could just reject them as
a coding error, it does not. Instead, it simply ignores the first one
(in general, it ignores all but the last assignment to a given signal
in situations like this). So, the signal B is wired to the signal
A, which is wired
to
the constant 0,
meaning that B is
also
wired to 0.
Note
that if we reversed the order of the two assignments to A, the meaning of the
specification (that is the circuit defined by the specification) would
change. So, while the order of signal assignments to A does matter, the
position of the assignment to B does not.
Note that we would not normally write the code fragment above in VHDL,
since it doesn't really make sense in the VHDL context. Also, it's
important to recognize that this code fragment is treated differently
if it lies
outside a process block. In that case, the output A is treated as though
it
is simultaneously wired to both a logic 1 and a logic 0. A
simulator
will typically show the value of A as being undefined and
a synthesizer will typically reject the circuit as physically
meaningless. (Of course, if the synthesizer were to synthesize a real
physical circuit as specified, and you applied power to it, the result
would be a short
circuit between power and ground, creating a small puff of smoke, an
unpleasant smell and a useless lump of silicon.)
Case Statements
VHDL provides a case statement that is useful for specifying different
results based on the value of a single signal. For example,
architecture a1 of foo is
begin
process(c,d,e) begin
b <= '1';
-- provide
default value for b
case e is
when "00"
=> a <= c; b <= d;
when "01"
=> a <= d; b <= c;
when "10"
=> a <= c xor d;
when others => a
<= '0';
end case;
end process;
end a1;
Anything you can do with a case
statement, you can also do with an if-then-else construct,
but often the case is
more convenient. Also, in those circumstances where it is appropriate,
a circuit synthesizer will generally produce a more efficient circuit
for a
case than it will
for an if-then-else.
For Loops
VHDL provides a for-loop
which is similar to the looping constructs in sequential programming
languages. We can use it to define repetitive circuits, like the adder
shown below. In this example, we also introduce the use of constants to
define
the size of the words that the adder operates on. The constant is
declared
in the package named commonConstants and is
referenced
by a use clause
before
the entity declaration. Packages are used to collect commonly used
declarations
in one place so that they can be used in different parts of the design.
It's a good practice to use named constants in this way, to make the
code
easier to understand and to facilitate making changes.
package commonConstants is
constant wordSize: integer :=
16;
end package commonConstants;
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
use work.commonConstants.all; -- makes package
visible to entity
entity
adder is
port(A, B: in
std_logic_vector(wordSize-1 downto 0);
Ci: in
std_logic;
S: out
std_logic_vector(wordSize-1 downto 0);
Co: out
std_logic
);
end adder;
architecture a1 of adder is
signal C: std_logic_vector(wordSize downto 0);
begin
process (A,B,C,Ci) begin
C(0) <= Ci;
for i in 0 to
wordSize-1 loop
S(i) <= A(i) xor B(i) xor C(i);
C(i+1) <= (A(i) and B(i)) or
((A(i)
xor B(i)) and C(i));
end loop;
Co <=
C(wordSize);
end process;
end a1;
The for-loop is equivalent to wordSize pairs of
assignments and while we could define the circuit that way, the loop is
certainly much more convenient and easier to understand. You might
wonder why we used a logic vector for the signal C. Wouldn't it be
simpler to write
architecture a1 of adder is
signal C: std_logic;
begin
process (A,B,C,Ci) begin
C <= Ci;
for i in 0
to wordSize-1 loop
S(i) <= A(i) xor B(i) xor C;
C <=
(A(i) and B(i)) or
((A(i)
xor B(i)) and C);
end loop;
Co <= C;
end process;
end a1;
While this makes perfect sense in a sequential programming languages it
does not have the intended meaning in VHDL, since there is no built-in
concept of sequential execution. The signal C can only be "wired"
one
way. It cannot be defined by different expressions at different times.
Consequently, the circuit defined by this specification will not behave
in the intended way.
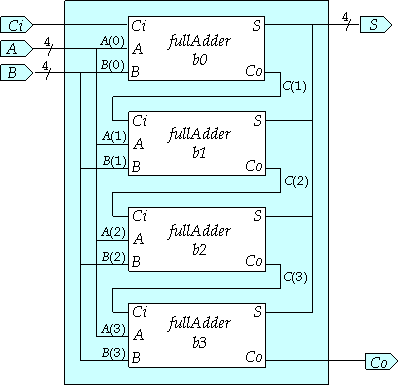
Structural VHDL
Larger circuits are generally implemented by combining large building
blocks together using what is known as structural VHDL. In
structural VHDL, we essentially "wire" together the different
components to form a larger circuit. We can illustrate this by
constructing a 4 bit adder using the full adder module defined earlier
as a building block.
entity
adder4 is
port(A, B:
in std_logic_vector(3 downto 0);
Ci: in
std_logic;
S: out
std_logic_vector(3 downto 0);
Co: out
std_logic
);
end adder4;
architecture a1 of adder4 is
-- local
component declaration for fullAdder
component fullAdder port(
A, B, Ci: in std_logic;
S, Co: out std_logic
);
end
component;
signal
C: std_logic_vector(3 downto 1);
begin
b0: fullAdder port map(A(0),B(0),Ci,S(0),C(1));
b1: fullAdder port
map(A(1),B(1),C(1),S(1),C(2));
b2: fullAdder port
map(A(2),B(2),C(2),S(2),C(3));
b3: fullAdder port map(A(3),B(3),C(3),S(3),Co);
end a1;
The meaning of this specification is illustrated in the block diagram
shown below.
Note that structural VHDL does not use a process construct. To use a
component within a VHDL architecture, you must include a local
component declaration as part of the architecture. The component
declaration defines the interface to the architecture and is similar to
the entity declaration. The component declaration is required even if
the entity declaration for the component is in the same file. This is
because VHDL requires that each architecture be self contained. The
four component instantiation statements specify the four
full adders. Each statement has a label that is used to distinguish the
components from one another. The port map portion of the
component instantiation statement defines which signals of the adder4 module are
associated with which ports of the fullAdder component. In
this case, we are using positional association of the ports.
That is, the position of a signal in the port map list determines which
signal in the component declaration it is associated with. VHDL also
allows
named association. For example, we could write
b0: fullAdder port
map(A=>A(0),B=>B(0),S=>S(0),
Ci=>Ci,C0=>C(1));
Note that if we use named association, the order in which the arguments
appear does not matter. For larger circuit
blocks with many inputs and outputs, named association is preferred.
Structural VHDL also supports iterative definitions so that we need not
write a whole series of similar component instantiation statements.
This allows us to write the four bit adder as
architecture a1 of adder4 is
-- local component declaration for fullAdder
component fullAdder port(
A, B, Ci: in std_logic;
S, Co: out std_logic
);
end
component;
signal
C: std_logic_vector(4 downto 0);
begin
C(0) <= Ci;
bg: for i
in 0 to 3 generate
b: fulladder
port map(A(i),B(i),C(i),S(i),C(i+1));
end generate;
Co <= C(4);
end a1;
Observe that in this version, we've declared C to be a five bit
signal, rather than a three bit signal and associated Ci with C(0) and Co with C(4). This avoids the
need for separate component instantiation statements for the first and
last
bits of the adder. The for-generate
statement also allows us to define the adder using a named constant for
the word size, instead of explicit values. This makes the code more
general and easier to change, if we decide that we need a different
word size. Note that the labels on the for-generate statement
and on the component instantiation statement are both required. Finally
we should point out that while we can use structural VHDL to define
circuits like the adder, usually it is more convenient to define
circuits like this with for-loops,
as discussed earlier. Structural VHDL is most useful for putting
together larger circuit blocks.
3. Sequential Circuits
What distinguishes sequential circuits from combinational circuits is
the fact that they can store values and retain them for later use.
Clocked sequential circuits store values in flip flops, most often,
edge-triggered D flip flops. VHDL provides a syncronization
condition for use in if-statements
that allows us to specify the storage of values in flip flops or
registers of flip flops. Here's an example.
if
rising_edge(clk) then
x <= a xor b;
end if;
The expression in the if-statement
is the syncronization condition. Here clk, is a clock signal.
The event
attribute is true whenever clk is changing. The
second part of the synchronization condition refers to the value of clk immediately after
the transition. So this synchronization condition says that the signal x should be assigned the
value a xor b on a
rising clock edge. To implement this behavior the circuit synthesizer
associates the signal x
with the output of a positive edge-triggered D flip flop. Note that
because x is the
output of a flip flop, it can only change when the flip flop changes.
This means
that all assignments to x
must be within the scope of if-statements with
identical synchronization condition. This requirement makes it
convenient to arrange one's VHDL specification so that all assignments
to signals whose values are stored in flip flops lie within the scope
of a single if-statement
containing the synchronization condition. In fact, while the language
doesn't require this, many circuit synthesizers cannot handle
specifications with more than one synchronization condition in the same
process. For this reason, we adopt the common convention of using at
most one synchronization condition in the processes used to specify
sequential circuits.
VHDL makes it easy to write a specification for a sequential circuit
directly from the state transition diagram for the circuit. The state
diagram shown below is for a sequential comparator with
two serial inputs, A
and B and two
outputs
G and L. There is also a reset input that
disables
the circuit and causes it to go the 00 state when it is high. After
reset
drops, the A and B inputs are
interpreted
as numerical values, with successive bits presented on successive clock
ticks, starting with the most significant bits. The G and L outputs are low
initially, but as soon as a difference is detected between the two
inputs,
one or the other of G
or L goes
high. Specifically, G
goes high if A>B
and L goes
high
if A<B. Notice
that
G and L go high before the
clock tick that causes the transition to the 10 and 01 states.
Here is a VHDL module that implements the comparator.
entity serialCompare is
Port (clk, reset: in std_logic;
A, B : in std_logic; -- inputs to be compared
G, L: out std_logic -- G means A>B,
L means A<B
);
end serialCompare;
architecture a1 of serialCompare is
signal state: std_logic_vector(0 to 1);
begin
-- process that defines state
transition
process(clk)
begin
if rising_edge(clk) then
if reset = '1' then
state <= "00";
elsif state = "00" then
if A = '1' and B = '0' then
state <= "10";
elsif A = '0' and B = '1' then
state <= "01";
end if;
end if;
end if;
end process;
-- process that defines the outputs
process(A, B, state) begin
G <= '0'; L <= '0';
if (state = "00"
and A = '1' and B = '0')
or state = "10" then
G <= '1';
end if;
if (state = "00"
and A = '0' and B = '1')
or state = "01" then
L <= '1';
end if;
end process;
end a1;
There are two processes in this specification. The first
defines the state transitions and starts with an if-statement containing
a synchronization condition. All assignments to the state signal occur
within
the scope of this if-statement
causing them to be synchronized to the rising edge of the clk signal. We start the
synchronized code segment by checking the status of reset and putting the
circuit into state 00 if reset is high, The
rest of the process controls the transition to the 10 or 01 states,
depending on which of the two inputs is larger. Notice that there is
no code for the "self-loops" in the transition diagram, since these
involve
no change to the state signal. The second process specifies the output
signals G and L. Although it's not
essential to define the outputs in a separate process, it's generally
considered
good practice to do so. Notice that this second process has no
synchronization condition and specifies a purely combinational
sub-circuit. The VHDL synthesizer analyzes this specification and
determines that the state
signal must be stored in a pair of flip flops. It also determines the
logic equations needed to generate the next state and output values and
uses these to create the required circuit. The diagram below shows a
circuit that could
be generated by the synthesizer from this specification.
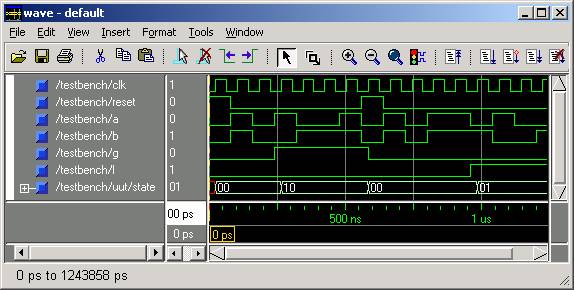
The figure below shows the output of a simulation run for the serial
comparator. Notice that the changes to the state variable are
synchronized to the rising clock edges but the the low-to-high
transitions of G
and L are not.
VHDL allows us to define signals with enumerated types allowing
us to associate meaningful names to values of signals. This is
particularly useful for naming the states of state machines, as
illustrated below.
architecture a1 of
serialCompare is
type stateType is (unknown, bigger, smaller);
signal state: stateType;
begin
-- process that defines state
transition
process(clk)
begin
if rising_edge(clk) then
if reset = '1' then
state <= unknown;
elsif state = unknown then
if A = '1' and B = '0' then
state <= bigger;
elsif A = '0' and B = '1' then
state <= smaller;
end if;
end if;
end if;
end process;
-- code that defines the outputs
G <= '1' when (state = unknown and A = '1' and B= '0')
or state = bigger else
'0';
L <= '1' when (state = unknown and A = '0' and B= '1')
or state = smaller else
'0';
end a1;
In this version, we have also defined the outputs with two conditional
signal assignments, instead of a process. In situations where the
outputs are fairly simple, this coding style is preferable.
Next, we look at an example of a more complex sequential circuit that
combines a small control state machine with a register to count the
number of "pulses" observed in a serial input bit stream, where a pulse
is defined as one or more clock ticks when the input is low, followed
by one or more clock ticks when it is high, followed by one or more
clock ticks when it is low. In addition to the data input A, the circuit has a reset input, which
disables and re-initializes the circuit. The primary output of the
circuit is the value of the four bit counter. There is also an error output which is
high if the input bit stream contains more than 15 pulses. If the
number of pulses observed exceeds 15, the counter "sticks" at 15. The
simplified state transition diagram shown below does not explicitly
include the
reset logic, which clears the counter and puts the circuit in the allOnes state. Also,
note
that the counter value us not shown explicitly, since this would
require
that the diagram include separate between and inPulse states for each
of the distinct counter values. Instead, we simply show whether the
counter is incremented or not.
Here is a VHDL module that implements pulse counter. In this example,
we have introduced two constants, one for the word size and another for
the maximum number of pulses that we can count. Note that because the
second constant has type
std_logic_vector, the package declaration requires the IEEE
library where the std_logic_vector
type is defined. Notice the correspondence between the transition
diagram and the code.
library
IEEE;
use IEEE.STD_LOGIC_1164.ALL;
package commonConstants is
constant wordSize: integer :=
4;
constant maxPulse:
std_logic_vector := "1111";
end package commonConstants;
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
use work.commonConstants.all;
-- Count the number of pulses in the input bit
stream.
-- A pulse is a 01...10 pattern.
entity countPulse is
Port (
clk,
reset: in std_logic;
A: in std_logic; -- input bit
stream
count: out
std_logic_vector(wordSize-1 downto 0);
errFlag: out
std_logic -- high if more than maxPulse detected
);
end countPulse;
architecture a1 of countPulse is
type stateType is (allOnes, between, inPulse,
errState);
signal state: stateType;
signal countReg: std_logic_vector(wordSize-1 downto
0);
begin
process(clk) begin
if rising_edge(clk) then
if reset = '1' then
countReg <= (others => '0');
state <= allOnes;
else
case state is
when allOnes =>
if A = '0'
then state <= between; end if;
when between =>
if A = '1'
then state <= inPulse; end if;
when inPulse =>
if A = '0' and
countReg /= maxPulse then
countReg <= countReg + "1";
state <= between;
elsif A = '0'
and countReg = maxPulse then
state <= errState;
end if;
when others =>
end case;
end if;
end if;
end process;
count <= countReg;
errFlag <= '1' when state =
errState else '0';
end a1;
Notice that we have defined a countReg signal separate
from the count
output signal because VHDL does not allow output signals to be used in
expressions. The standard way to get around this is to have an internal
signal that is manipulated within the module and then assign the value
of this internal signal to the output signal. Also notice the
assignment to countReg
in the reset section.
countReg <= (others => '0');
This means that all bits of the countReg are 0. We could have written
countReg <= "0000";
but this makes the code dependent on the word size, which we would
prefer to avoid.
The countPulse
circuit illustrates a common characteristic of many sequential
circuits. While strictly speaking, the state of the circuit consists of
both the state
signal and the value of countReg,
the two serve somewhat different purposes. The state signal keeps tack
of the control state of the circuit while the countReg variable holds
the data state. We can generally simplify the state transition
diagram for a sequential circuit by representing only the
control state explicitly while indicating the modifications to the data
state as though they were outputs to the circuit. This leads directly
to a VHDL representation based directly on the transition diagram.
We finish this section with a larger sequential circuit that implements
a hardware priority queue. A priority queue
maintains a set of (key,value) pairs. Its primary output
is called smallValue
and it is equal to the value of the pair that has the smallest key.
So for example, if the priority queue contained the pairs (2,7), (1,5)
and (4,2) then the smallValue
output would be 5. There are two operations that can be performed on
the priority queue. An insert operation adds a new (key,value)
pair to the set of stored pairs. A delete operation removes the (key,value)
pair with the smallest key from the set. The circuit has the following
inputs.
clk the clock signal
reset initializes the
circuit, discarding any stored values that may be present
insert when high, it initiates an insert operation
delete when high, it initiates a delete operation;
however, if insert and delete are
high at the same time,
then the delete signal is ignored
key the key part of a new pair being
inserted
value the value part of a new pair being
inserted
The circuit has the following outputs, in addition to smallValue.
busy
is high when the circuit is in the middle of performing an
operation;
while busy is high, the insert and delete inputs are ignored; the
outputs are not required to have the correct values when busy is high
empty
is high when there are no pairs stored in the priority queue; delete
operations are ignored in this case
full
is high when there is no room for any additional pairs to be
stored;
insert operations are ignored in this case
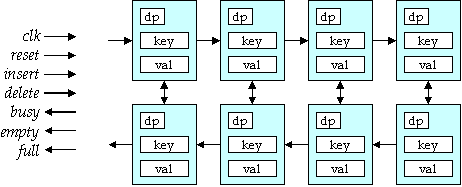
The figure below shows a block diagram for one implementation of a
priority queue.
In this design, there is a set of blocks arranged in two rows. Each
block contains two registers, one storing a key, the other storing a
value. In addition, there is a flip flop called dp, which stands for
data
present. This bit is set for every block that contains a valid (key,value)
pair. The circuit maintains the set of stored pairs so that three
properties are maintained.
- For adjacent pairs in the bottom row, the pair to the
left has a key that is less than or equal to that of the pair on the
right.
- For pairs that are in the same column, the key of the
pair in the bottom row is less than or equal to that of the pair in
the top row.
- In both rows, the empty blocks (those with dp=0) are to the right
and either both rows have the same number of empty blocks or the top
row has one more than the bottom row.
When these properties hold, the pair with the smallest key is in the
leftmost block of the bottom row. Using this organization, it is
straightforward to implement the insert and delete operations. To
do an insert, the (key,value) pairs in the top row are
all shifted to the right one position, allowing the new pair to be
inserted in the leftmost block of the top row. Then, within each
column, the keys of the pairs in those columns are compared, and if
necessary, the pairs are swapped to maintain properties 2 and 3. Note
that the entire operation takes two steps. While it is in progress, the
busy output is high. The
delete operation is similar. First, the pairs in the bottom row are all
shifted to the left, effectively deleting the pair with the smallest
key.
Then, for each column, the key values are compared and if necessary,
the
pairs are swapped to maintain properties 2 and 3. Given these
properties, we can determine if the priority queue is full by checking
the rightmost dp
bit in the top row and we can determine if it is empty by checking the
leftmost dp
bit in the bottom row.
The complete state of this circuit includes all the values stored in
all the registers, but we can express the control state is much more
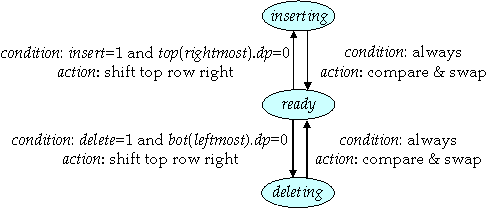
simply, as shown in the transition diagram below.
This is a somewhat conceptual state transition diagram, but it captures
the essential behavior we want. In particular, the labels on the arrows
indicate the condition that causes the given transition to
take place and any action that should be performed at the same
time.
The variable top(rightmost).dp refers to the
rightmost data present flip flop in the top row and bot(leftmost).dp
refers to the leftmost data present flip flop in the bottom row. In the
ready state, the circuit is between operations and waiting for
the next operation. If it gets an insert request and it is not full, it
goes to the inserting state and shifts the new (key,value)
pair into the top row and shifts the whole row right. From there it
makes a transition back to the ready state while doing a
"compare
& swap" between all vertical pairs. If the circuit gets a delete
request when it is in the ready state and is not empty, it goes
to the deleting state and shifts the bottom row to the left.
From
there, it immediately returns to the ready state, whild
performaning
a compare & swap.
A VHDL module implementing this design is shown below.
--
Priority Queue module implements a priority queue storing
-- up to 8 (key,value) pairs. The keys
and values are 4 bits
-- each. When the priority queue is not
empty, the output
-- smallValue is the value of a pair with the
smallest key.
-- The empty and full outputs report the status of the
priority
-- queue. The busy output remains high while an insert or
-- delete operation is in progress. While it is high, new
-- operation requests are ignored
entity
priQueue is
Port
(clk, reset : in std_logic;
insert, delete : in std_logic;
key, value : in
std_logic_vector(wordSize-1 downto 0);
smallValue : out std_logic_vector(wordSize-1 downto 0);
busy, empty, full : out std_logic
);
end priQueue;
architecture a1 of
priQueue is
constant rowSize:
integer := 4; -- local constant declaration
type pqElement is record
dp:
std_logic;
key:
std_logic_vector(wordSize-1 downto 0);
value: std_logic_vector(wordSize-1 downto 0);
end record pqElement;
type rowTyp is array(0
to rowSize-1) of pqElement;
signal top, bot: rowTyp;
type state_type is
(ready, inserting, deleting);
signal state: state_type;
begin
process(clk) begin
if rising_edge(clk) then
if reset = '1' then
for i in 0 to
rowSize-1 loop
top(i).dp <= '0'; bot(i).dp <= '0';
end loop;
state <=
ready;
elsif state = ready and insert =
'1' then
if
top(rowSize-1).dp /= '1' then
for i in 1 to rowSize-1 loop
top(i) <= top(i-1);
end loop;
top(0) <= ('1',key,value);
state <= inserting;
end if;
elsif state = ready and delete =
'1' then
if bot(0).dp
/= '0' then
for i in 0 to rowSize-2 loop
bot(i) <= bot(i+1);
end loop;
bot(rowSize-1).dp <= '0';
state <= deleting;
end if;
elsif state = inserting or state
= deleting then
for i in 0 to
rowSize-1 loop
if top(i).dp = '1' and
(top(i).key < bot(i).key
or
bot(i).dp = '0') then
bot(i) <= top(i); top(i) <=
bot(i);
end if;
end loop;
state <=
ready;
end if;
end if;
end
process;
smallValue <= bot(0).value when bot(0).dp = '1' else
(others => '0');
empty
<= not bot(0).dp;
full
<= top(rowSize-1).dp;
busy
<= '1' when state /= ready else '0';
end a1;
This example illustrates the use of arrays of records to represent the
two rows in the priority queue. The code segment
type
pqElement is record
dp: std_logic;
key: std_logic_vector(wordSize-1
downto 0);
value:
std_logic_vector(wordSize-1 downto 0);
end record pqElement;
defines the basic building block of the arrays. We can refer to
elements of the arrays or specific fields of specific elements using
expressions like
top(i) bot(i).value
Note how the use of the use of these arrays allows us to express the
design of the circuit in a way that directly reflects the high level
description.
Sequential circuits can be used to build systems of great
sophistication and complexity. The challenge, to the designer is to
manage that complexity so as not to be overwhelmed by it. VHDL is one
important tool that can help in meeting the challenge, but to use it
effectively, you need to learn the common patterns that experience has
shown are most useful in expressing the functionality of digitial
systems. This section has introduced some of the more useful patterns.
You should study the examples carefully to make
sure you understand how they work and to develop a familiarity with the
patterns they follow.
4. Functions and Procedures
Like conventional programming languages, VHDL provides a subroutine
mechanism to allow you to encapusulate circuit components that are used
repeatedly in different contexts. The example below shows how a
function can be used to represent a circuit that finds the first 1 in a
logic
vector.
entity
firstOne is
Port (a: in std_logic_vector(0 to wordSize-1);
x:
out std_logic_vector (0 to wordSize-1)
);
end firstOne;
architecture a1 of frstOne is
function firstOne(x: std_logic_vector(0 to wordSize-1))
return std_logic_vector
is
-- Returns a bit vector with a 1 in the position
where
-- the first one in the input bit string is found
-- everywhere else, it is zero
variable allZero: std_logic_vector(0 to wordSize-1);
variable fOne: std_logic_vector(0 to wordSize-1);
begin
allZero(0) := not x(0);
fOne(0) := x(0);
for i in 1 to wordSize-1 loop
allZero(i) := (not
x(i)) and allZero(i-1);
fOne(i) :=
x(i) and allZero(i-1);
end loop;
return fOne;
end function firstOne;
begin
x <= firstOne(a);
end a1;
Note that within the function definition, we can use the for-loop and other
complex statements. Also, note that within the function we use
variables not signals. When the function is invoked, the variables will
be associated with signals in the context from which the function is
invoked, but within the function definition, we use variables. When
assigning a value to a
variable, we must use the variable assignment operator :=.
We can use procedures to specify common subcircuits that produce more
than one output. In the example shown below, the firstOne function has
been modified so that it returns the numerical index of the first 1 in
the argument bit string, instead of a bit vector that marks the
position of the first 1. It is implemented using a separate encode procedure which
has two output parameters, one for the index, and the other for an
error flag. The firstOne
function inserts the error flag into the high order bit of its return
value.
package
commonConstants is
constant lgWordSize: integer := 4;
constant wordSize: integer := 2**lgWordSize;
end package
commonConstants;
library IEEE;
use
IEEE.STD_LOGIC_1164.ALL;
use
IEEE.STD_LOGIC_ARITH.ALL;
use
IEEE.STD_LOGIC_UNSIGNED.ALL;
use
work.commonConstants.all;
entity firstOne is
Port
(a: in std_logic_vector(0 to wordSize-1);
x: out std_logic_vector (lgWordSize
downto 0)
);
end firstOne;
architecture a1 of
firstOne is
procedure encode(x: in
std_logic_vector(0 to wordSize-1);
indx: out std_logic_vector(lgWordSize-1 downto 0);
errFlag: out std_logic) is
-- Unary to binary
encoder.
-- Input x is assumed to
have at most a single 1 bit.
-- Indx is equal to the
index of the bit that is set.
-- If no bits are set,
errFlag bit is made high.
-- This is conceptually
simple.
--
--
indx(0) is OR of x(1),x(3),x(5), ...
--
indx(1) is OR of x(2),x(3), x(6),x(7), x(10),x(11),
...
--
indx(2) is OR of x(4),x(5),x(6),x(7),
x(12),x(13),x(14(,x(15),...
--
-- but it's tricky to
code so it works for different word sizes.
type vec is array(0 to
lgWordSize-1) of std_logic_vector(0 to (wordSize/2)-1);
variable fOne: vec;
variable anyOne:
std_logic_vector(0 to wordSize-1);
begin
--
fOne(0)(j) is OR of first j bits in x1,x3,x5,...
--
fOne(1)(j) is OR of first j bits in x2,x3, x6,x7, x10,x11,...
--
fOne(2)(j) is OR of first j bits in x4,x5,x6,x7, x12,x13,x14,x15,...
for i
in 0 to lgWordSize-1 loop
for j in 0 to (wordSize/(2**(i+1)))-1
loop
for h in 0 to (2**i)-1 loop
if j = 0 and h
= 0 then
fOne(i)(0) := x(2**i);
else
fOne(i)((2**i)*j+h) := fOne(i)((2**i)*j+h-1) or
x(((2**i)*(2*j+1))+h);
end if;
end loop;
end loop;
indx(i) := fOne(i)((wordSize/2)-1);
end
loop;
anyOne(0) := x(0);
for i
in 1 to wordSize-1 loop
anyOne(i) := anyOne(i-1) or x(i);
end
loop;
errFlag := not anyOne(wordSize-1);
end procedure encode;
function firstOne(x:
std_logic_vector(0 to wordSize-1))
return std_logic_vector is
-- Returns the index of
the first 1 in bit string x.
-- If there are no 1's
in x, the value returned has a
-- 1 in the high order
bit.
variable allZero:
std_logic_vector(0 to wordSize-1);
variable fOne:
std_logic_vector(0 to wordSize-1);
variable rslt:
std_logic_vector(lgWordSize downto 0);
begin
allZero(0) := not x(0);
fOne(0) := x(0);
for i
in 1 to wordSize-1 loop
allZero(i) := (not x(i)) and allZero(i-1);
fOne(i) := x(i) and allZero(i-1);
end
loop;
encode(fOne,rslt(lgWordSize-1 downto 0),rslt(lgWordSize));
return rslt;
end function firstOne;
begin
x
<= firstOne(a);
end a1;
Functions and procedures can be important components of a larger VHDL
circuit design. They eliminate much of the repetition that can occur in
larger designs, facilitate re-use of design elements developed by
others and can make large designs easier to understand and manage.
5. Closing Remarks
This tutorial is just an introduction to VHDL and makes no attempt to
be comprehensive. VHDL is a large, complex language with a great many
features that while useful in some contexts, are not essential to the
development of smaller digital systems. There are a great many books
describing VHDL that you'll find useful as you progress through later
courses and apply VHDL to more complex systems. As you learn more about
the language, you will
discover that using VHDL to synthesize circuits is only one of its
uses.
In fact, the original purpose of the language was to model digital
systems
in software, to enable rapid simulation and evaluation of architectural
alternatives before proceeding with a specific design. The development
of
circuit synthesizers that could convert VHDL specifications into actual
hardware descriptions came later, only after the language was in
wide-spread use for modelling and simulation. As a result of this
history, it's possible to write VHDL specifications that, while they
can be simulated, cannot be synthesized. In this tutorial, we have
emphasized synthesizable VHDL specifications, and indeed, all the
examples in this tutorial can be (and have been) synthesized.
Last updated 1/2/05.